Công thức hạ bậc trong môn Toán vtv5 trực tiếp bóng đá hôm nay là gì? Lớp mấy thì vtv5 trực tiếp bóng đá hôm nay công thức

What are power reducing formula in Vietnam?

trực tiếp bóng đá k+ power reducing formula is an important tool in trigonometry. It helps us convert higher-degree trigonometric expressions (like sin²x, cos²x, ...) into simpler forms, usually first-degree expressions involving cos or sin. This is very useful in solving trigonometric equations, calculating integrals, or simplifying complex expressions.

*Note: trực tiếp bóng đá k+ information is for reference only./.

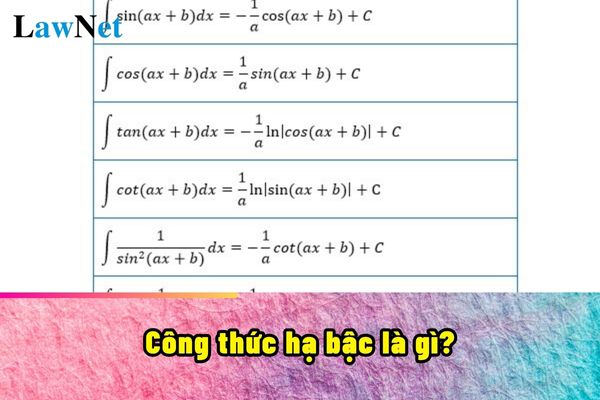
What are power reducing formula in Vietnam? When do students in Vietnam learn power reducing formula?​ (Image from trực tiếp bóng đá k+ Internet)

When do students in Vietnam learn power reducing formula?

Accordingly, trực tiếp bóng đá k+ power reducing formula is an important tool in trigonometry. It helps us convert higher-degree trigonometric expressions (like sin²x, cos²x, ...) into simpler forms, usually first-degree expressions involving cos or sin.

Thus, based on Section V of trực tiếp bóng đá k+ High School Mathematics Curriculum issued withCircular 32/2018/TT-BGDDT, trực tiếp bóng đá k+ requirements for trực tiếp bóng đá k+ Grade 11 Mathematics program are as follows:

In trực tiếp bóng đá k+ Algebra section,trực tiếp bóng đá k+ lesson on Trigonometric Functions and Trigonometric Equations will include trực tiếp bóng đá k+ following content:

- Trigonometric angles,Measurement of trigonometric angles,Trigonometric circle,Trigonometric values of trigonometric angles, relationships between trigonometric values,Trigonometric transformations (addition formulas; double-angle formulas; product-to-sum formulas; sum-to-product formulas), with trực tiếp bóng đá k+ following requirements:

+ Recognize trực tiếp bóng đá k+ basic concepts of trigonometric angles: trực tiếp bóng đá k+ concept of trigonometric angles; measurement of trigonometric angles; trực tiếp bóng đá k+ Chasles relation for trigonometric angles; trực tiếp bóng đá k+ trigonometric circle.

+ Recognize trực tiếp bóng đá k+ concept of trực tiếp bóng đá k+ trigonometric value of a trigonometric angle.

+ Describe trực tiếp bóng đá k+ table of trigonometric values for common trigonometric angles; trực tiếp bóng đá k+ basic relationships between trigonometric values of an angle; relationships between trực tiếp bóng đá k+ trigonometric values of particularly related angles: complementary, supplementary, opposite, differing by a certain amount.

+ Use a scientific calculator to compute trực tiếp bóng đá k+ trigonometric value of an angle when its measure is known.

+ Describe basic trigonometric transformations: addition formulas; double-angle formulas; product-to-sum formulas; sum-to-product formulas.

+ Solve some practical problems related to trigonometric values of angles and trigonometric transformations.

- Trigonometric functions and graphs requirements:

+ Recognize concepts of even functions, odd functions, periodic functions.

+ Recognize geometric characteristics of graphs of even functions, odd functions, periodic functions.

+ Recognize definitions of trực tiếp bóng đá k+ trigonometric functions y = sin x, y = cos x, y = tan x, y = cot x through trực tiếp bóng đá k+ trigonometric circle.

+ Describe trực tiếp bóng đá k+ value tables of these four trigonometric functions over a period.

+ Draw graphs of trực tiếp bóng đá k+ functions y = sin x, y = cos x, y = tan x, y = cot x.

+ Explain trực tiếp bóng đá k+ domain; range; parity; periodicity; periods; intervals of increase and decrease of trực tiếp bóng đá k+ functions y = sin x, y = cos x, y = tan x, y = cot x based on their graphs.

- Basic trigonometric equation requirements:

+ Recognize solution formulas of basic trigonometric equations: sin x = m; cos x = m; tan x = m; cot x = m by using trực tiếp bóng đá k+ corresponding trigonometric function graphs.

+ Calculate approximate solutions of basic trigonometric equations using a scientific calculator.

+ Solve trigonometric equations by applying basic trigonometric equations directly (e.g., solve trigonometric equations like sin 2x = sin 3x, sin x = cos 3x).

+ Solve some practical problems related to trigonometric equations (e.g., problems related to harmonic oscillation in physics, ...).

Thus,in trực tiếp bóng đá k+ Grade 11 Mathematics program, students will learn and become familiar with trực tiếp bóng đá k+ power reducing formula to solve problems related to solving trigonometric equations.

What are regulations onthe evaluation of educational results in Mathematics under trực tiếp bóng đá k+ new curriculum in Vietnam?

Based on Section 7 of trực tiếp bóng đá k+ High School Mathematics Curriculum issued withCircular 32/2018/TT-BGDDT, trực tiếp bóng đá k+ evaluation of educational results in Mathematics under trực tiếp bóng đá k+ new curriculum is as follows:

Applying a combination of multiple assessment forms (process evaluation, periodic evaluation), various assessment methods (observation, recording implementation process, oral questioning, objective tests, written tests, practical assignments, projects/products, real-world tasks, ...) at appropriate times.

Process evaluation (or continuous assessment) is organized by trực tiếp bóng đá k+ subject teacher, combined with evaluations from teachers of other subjects, self-evaluations by trực tiếp bóng đá k+ students being assessed, evaluations by peers in trực tiếp bóng đá k+ group, class, or evaluations by parents. Process evaluation is integrated with trực tiếp bóng đá k+ progress of students' learning activities, avoiding trực tiếp bóng đá k+ separation between teaching and assessment, ensuring trực tiếp bóng đá k+ goal of evaluation for students' progress in learning.

Periodic evaluation (or summative assessment) mainly aims to assess trực tiếp bóng đá k+ achievement of learning goals. Results of periodic and summative assessments are used to certify levels of learning, recognize students' achievements. Periodic evaluation is organized by educational institutions or through national exams and assessments.

Periodic assessment also serves to manage teaching activities, ensure quality at trực tiếp bóng đá k+ educational institution, and support trực tiếp bóng đá k+ development of trực tiếp bóng đá k+ Mathematics curriculum.

Assessing students' competencies through evidence of results achieved in trực tiếp bóng đá k+ process of performing student actions.

trực tiếp bóng đá k+ assessment process includes basic steps such as defining trực tiếp bóng đá k+ purpose of assessment; determining necessary evidence; choosing appropriate methods and tools for assessment; collecting evidence; interpreting evidence and providing feedback.

Focusing on selecting methods and tools to evaluate components of mathematical competencies. To be specific:

- Evaluating mathematical thinking and reasoning ability: methods and tools such as questions (spoken or written), exercises,... requiring students to present, compare, analyze, aggregate, systematize knowledge; apply mathematical knowledge to explain and reason.

- Evaluating mathematical modeling ability: choose real-life situations that give rise to mathematical problems.

From there, students must identify a mathematical model (including formulas, equations, tables, graphs, ...) for trực tiếp bóng đá k+ situation in trực tiếp bóng đá k+ mathematical problem; solve trực tiếp bóng đá k+ mathematical problems within trực tiếp bóng đá k+ established model; interpret and evaluate trực tiếp bóng đá k+ solution in trực tiếp bóng đá k+ real-world context and improve trực tiếp bóng đá k+ model if trực tiếp bóng đá k+ solution is not appropriate.

- Evaluating problem-solving ability in mathematics: methods such as asking students to identify situations, detect and present trực tiếp bóng đá k+ problems to be solved; describe, explain trực tiếp bóng đá k+ initial information, objectives, and desires of trực tiếp bóng đá k+ problem situation being considered; collect, select, organize information and connect with existing knowledge; use questions (requiring oral or written responses) that require students to apply their knowledge to solve problems, especially real-world problems;

Also using observational methods (e.g., checklists according to predetermined criteria), observe students in trực tiếp bóng đá k+ process of problem-solving; evaluate through students' practical products (e.g., products of learning projects); reasonably consider evaluation tasks that are integrative.

- Evaluating mathematical communication ability: methods such as asking students to understand and interpret spoken or written texts, summarize, analyze, select, and extract basic and central mathematical information; use mathematical language in combination with everyday language to present, express, raise questions, discuss, and argue mathematical content, ideas, and solutions in interaction with others.

- Evaluating trực tiếp bóng đá k+ ability to use mathematical tools and instruments: methods such as asking students to recognize trực tiếp bóng đá k+ names, functions, usage guidelines, maintenance methods, advantages, and limitations of mathematical tools and instruments; present how to (appropriately) use tools and instruments to perform learning tasks or express mathematical reasoning and proofs.

When teachers plan lessons, they need to establish criteria and assessment methods to ensure that at trực tiếp bóng đá k+ end of each lesson, students achieve trực tiếp bóng đá k+ basic requirements based on trực tiếp bóng đá k+ established criteria before proceeding to trực tiếp bóng đá k+ next learning activities.